Description

The Software Project Scheduling problem consists in deciding who does what during the software project lifetime. There exists a set of employees that have to complete a set of tasks. Each employee has a salary and some skills. The tasks are related by a Task Precedence Graph (TPG), wich determines a partial ordering in the set of tasks. The main two objectives are to reduce the completion time and the cost of the whole project. Below we present a detailed description of the problem.

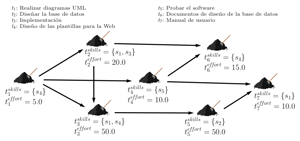
The resources considered are people with a set of skills, a salary, and a maximum dedication to the project. Formally, each person (employee) is denoted with e_i where i goes from 1 to E (the number of employees). Let SK be the set of skills, and s_i the i-th skill for i varying from 1 to S=|SK|. The skills of the employee e_i will be denoted with e_i^sk that is a subset of SK, the monthly salary with e_i^sa, and the maximum dedication to the project with e_i^md. The salary and the maximum dedication are both real numbers. The former is expressed in fictitious currency units, while the latter is the ratio between the amount of hours dedicated to the project and the full working day length of the employee. For example, a maximum dedication of 0.75 means that the employee spends at most 75% of its working day to tasks of the project. A maximum dedication greater than 1.0 means that the employee can work overtime.

The tasks are denoted with t_i for i from 1 to T (the number of tasks). Each task t_i has a set of required skills associated to it that we denote with t_i^sk and an effort t_i^ef expressed in person-month (PM). The tasks must be performed according to a TPG. The TPG indicates what tasks must be completed before the beginning of a new task. The TPG is an acyclic directed graph G(V,A) with a vertex set V={t₁, t₂, ..., t_T} and an arc set A where (t_i, t_j) belongs to A if the task t_i must be completed, with no other intervening tasks, before task t_j can start.

Our objectives are to minimize the cost, the duration of the project, and the overtime of the employees. The constraints are that each task must be performed by at least one person and the set of required skills of a task must be included in the union of the skills of the employees performing the task. Once we know the elements of a problem instance, let us proceed to describe the elements of a solution to the problem. A solution can be represented with a matrix X=(x_ij) of size ExT. The element x_ij is the dedication degree of the employee e_i to the task t_j. If the employee e_i performs the task t_j with a 0.5 dedication degree s/he spends half of his/her working day in the task. If an employee does not perform a task s/he will have a dedication degree of 0 to that task. This information helps to compute the duration of each task and, indeed, the start and end time of each one, i.e., the time schedule of the tasks. From this schedule we can compute the duration of the project. The cost can be calculated after the duration of the tasks accounting also for the dedication and salary of the employees. Finally, the overtime of each employee can be calculated using the time schedule of the tasks and the dedication matrix X.

Variants

The problem presented above can be made more realistic in different ways. Adding new elements to the problem description we have new variants of the problem that are briefly described in the following:

Instance generator

We have developed an instance generator for this problem. Click here to see the description of the generator and to get some generated instances.

Instances for Scalability Analysis

We have generated instances with 8 to 256 employees and 16 to 512 tasks in order to study the scalability properties of the search algorithms. In total we have 36 instances that can be downloaded from this link.

Related Bibliography and Papers